A* 算法

BraumAce2024年8月5日约 3955 字大约 13 分钟

A* 算法

1. 介绍

$A*$ （念做：A Star）算法是一种很常用的路径查找和图形遍历算法。它有较好的性能和准确度。

2. 搜索

2.1 广度优先搜索

广度优先搜索以广度做为优先级进行搜索。

从起点开始，首先遍历起点周围邻近的点，然后再遍历已经遍历过的点邻近的点，逐步的向外扩散，直到找到终点。

这种算法就像洪水（ $Flood fill$ ）一样向外扩张。

对于有明确终点的问题来说，一旦到达终点便可以提前终止算法，下面这幅图对比了这种情况：

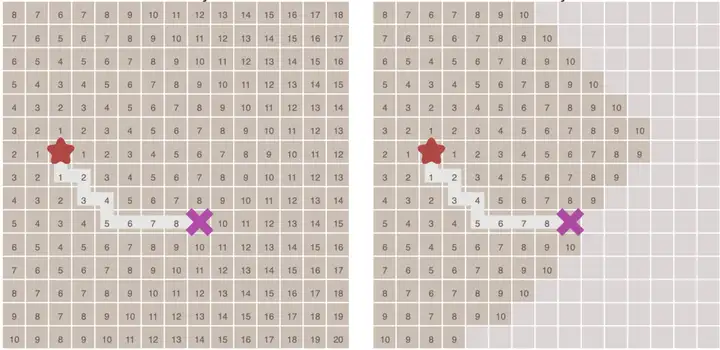
在执行算法的过程中，每个点需要记录达到该点的前一个点的位置 -- 可以称之为父节点。这样做之后，一旦到达终点，便可以从终点开始，反过来顺着父节点的顺序找到起点，由此就构成了一条路径。

2.2 Dijkstra 算法

$Dijkstra$ 算法用来寻找图形中节点之间的最短路径。

考虑这样一种场景，在一些情况下，图形中相邻节点之间的移动代价并不相等。例如，游戏中的一幅图，既有平地也有山脉，那么游戏中的角色在平地和山脉中移动的速度通常是不相等的。

在 $Dijkstra$ 算法中，需要计算每一个节点距离起点的总移动代价。同时，还需要一个优先队列结构。对于所有待遍历的节点，放入优先队列中会按照代价进行排序。

在算法运行的过程中，每次都从优先队列中选出代价最小的作为下一个遍历的节点。直到到达终点为止。

注意

当图形为网格图，并且每个节点之间的移动代价是相等的，那么 $Dijkstra$ 算法将和广度优先算法变得一样。

2.3 最佳优先搜索

在一些情况下，如果我们可以预先计算出每个节点到终点的距离，则我们可以利用这个信息更快的到达终点。

其原理也很简单。与 $Dijkstra$ 算法类似，我们也使用一个优先队列，但此时以每个节点到达终点的距离作为优先级，每次始终选取到终点移动代价最小（离终点最近）的节点作为下一个遍历的节点。这种算法称之为最佳优先（ $Best First$ ）算法。可以大大加快路径的搜索速度。

但是算法也有缺点，如果起点和终点之间存在障碍物，则最佳优先算法找到的很可能不是最短路径。

3. A*

$A*$ 算法通过下面这个函数来计算每个节点的优先级。

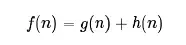
其中：

$f(n)$ 是节点 $n$ 的综合优先级。当我们选择下一个要遍历的节点时，我们总会选取综合优先级最高（值最小）的节点。
$g(n)$ 是节点 $n$ 距离起点的代价。
$h(n)$ 是节点 $n$ 距离终点的预计代价，即 $A*$ 算法的启发函数。

$A*$ 算法在运算过程中，每次从优先队列中选取 $f(n)$ 值最小（优先级最高）的节点作为下一个待遍历的节点。

另外， $A*$ 算法使用两个集合来表示待遍历的节点，与已经遍历过的节点，这通常称之为 open_set 和 close_set。

完整的 $A*$ 算法描述如下：

* 初始化 open_set 和 close_set；
* 将起点加入 open_set 中，并设置优先级为 0（优先级最高）；
* 如果 open_set 不为空，则从 open_set 中选取优先级最高的节点 n：
    * 如果节点 n 为终点，则：
        * 从终点开始逐步追踪 parent 节点，一直达到起点；
        * 返回找到的结果路径，算法结束；
    * 如果节点 n 不是终点，则：
        * 将节点 n 从 open_set 中删除，并加入 close_set 中；
        * 遍历节点 n 所有的邻近节点：
            * 如果邻近节点 m 在 close_set 中，则：
                * 跳过，选取下一个邻近节点
            * 如果邻近节点 m 在 open_set 中，则：
            	* 比较 gcost 是否比原来更小
            	* 如果更小则更新 parent
            * 如果邻近节点 m 也不在 open_set 中，则：
                * 设置节点 m 的 parent 为节点 n
                * 计算节点 m 的优先级
                * 将节点 m 加入 open_set 中

4. 启发函数

启发函数会影响 $A*$ 算法的行为。

在极端情况下，当启发函数 $h(n)$ 始终为0，则将由 $g(n)$ 决定节点的优先级，此时算法就退化成了 $Dijkstra$ 算法。
如果 $h(n)$ 始终小于等于节点 $n$ 到终点的代价，则 $A*$ 算法保证一定能够找到最短路径。但是当 $h(n)$ 的值越小，算法将遍历越多的节点，也就导致算法越慢。
如果 $h(n)$ 完全等于节点 $n$ 到终点的代价，则 $A*$ 算法将找到最佳路径，并且速度很快。可惜的是，并非所有场景下都能做到这一点。因为在没有达到终点之前，我们很难确切算出距离终点还有多远。
如果 $h(n)$ 的值比节点 $n$ 到终点的代价要大，则 $A*$ 算法不能保证找到最短路径，不过此时会很快。
在另外一个极端情况下，如果 $h(n)$ 相较于 $g(n)$ 大很多，则此时只有 $h(n)$ 产生效果，这也就变成了最佳优先搜索。

由上面这些信息我们可以知道，通过调节启发函数我们可以控制算法的速度和精确度。因为在一些情况，我们可能未必需要最短路径，而是希望能够尽快找到一个路径即可。这也是 $A*$ 算法比较灵活的地方。

对于网格形式的图，有以下这些启发函数可以使用：

如果图形中只允许朝上下左右四个方向移动，则可以使用 曼哈顿距离 （ $Manhattan \ distance$ ）。
如果图形中允许朝八个方向移动，则可以使用 对角距离。
如果图形中允许朝任何方向移动，则可以使用 欧几里得距离（ $Euclidean \ distance$ ）。

5. 关于距离

5.1 曼哈顿距离

如果图形中只允许朝上下左右四个方向移动，则启发函数可以使用曼哈顿距离，它的计算方法如下图所示：

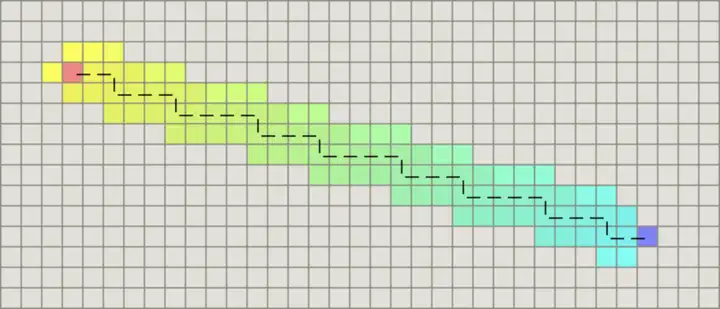
计算曼哈顿距离的函数如下，这里的D是指两个相邻节点之间的移动代价，通常是一个固定的常数。

function heuristic(node) =
    dx = abs(node.x - goal.x)
    dy = abs(node.y - goal.y)
    return D * (dx + dy)

5.2 对角距离

如果图形中允许斜着朝邻近的节点移动，则启发函数可以使用对角距离。它的计算方法如下：

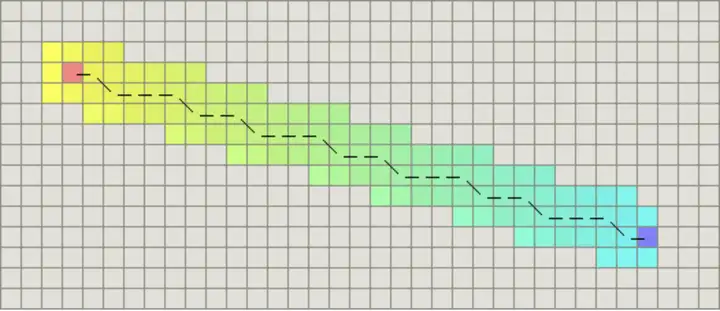
计算对角距离的函数如下，这里的 D2 指的是两个斜着相邻节点之间的移动代价。如果所有节点都正方形，则其值就是

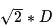
function heuristic(node) =
    dx = abs(node.x - goal.x)
    dy = abs(node.y - goal.y)
    return D * (dx + dy) + (D2 - 2 * D) * min(dx, dy)

5.3 欧几里得距离

如果图形中允许朝任意方向移动，则可以使用欧几里得距离。

欧几里得距离是指两个节点之间的直线距离，因此其计算方法也是我们比较熟悉的：

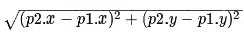
其函数表示如下：

function heuristic(node) =
    dx = abs(node.x - goal.x)
    dy = abs(node.y - goal.y)
    return D * sqrt(dx * dx + dy * dy)

6.补充

1. A* 应用场景:
起点 → 终点的最短距离
状态空间 >> 1e10 
启发函数减小搜索空间

2. A* 算法:
while(q.size())
    t ← 优先队列的队头  小根堆
        当终点第一次出队时 break;
        从起点到当前点的真实距离 d_real
        从当前点到终点的估计距离 d_estimate
        选择一个估计距离最小的点 min(d_estimate)
    for j in ne[t]:
        将邻边入队

3. A* 算法条件:
估计距离 <= 真实距离

d[state] + f[state] = 起点到state的真实距离 + state到终点的估计距离=估计距离
                                                                    ^
d[state] + g[state] = 起点到state的真实距离 + state到终点的真实距离=真实距离

一定是有解才有 d[i] >= d[最优] = d[u]+f[u]
              f[u] >= 0

4. 证明终点第一次出队列即最优解

(1)假设终点第一次出队列时不是最优 
   则说明当前队列中存在点u
     有 d[估计]< d[真实]
   d[u] + f[u] <= d[u] + g[u] = d[队头终点]
   即队列中存在比d[终点]小的值

(2)但我们维护的是一个小根堆, 没有比d[队头终点]小的d[u], 矛盾, 证毕.

5. A* 不用判重
   以边权都为1为例
   A o→o→o
     ↑   ↓
   S o→o→o→o→o→o→o T
       B
   dist[A] = dist[S]+1 + f[A] = 7
   dist[B] = dist[S]+1 + f[B] = 5
   则会优先从B这条路走到T
   B走到T后再从A这条路走到T

7. 例题

7.1 第k短路

给定一张 $N$ 个点（编号 $1,2…N$ ）， $M$ 条边的有向图，求从起点 $S$ 到终点 $T$ 的第 $K$ 短路的长度，路径允许重复经过点或边。

注意： 每条最短路中至少要包含一条边。

输入格式

第一行包含两个整数 $N$ 和 $M$ 。
接下来 $M$ 行，每行包含三个整数 $A,B$ 和 $L$ ，表示点 $A$ 与点 $B$ 之间存在有向边，且边长为 $L$ 。
最后一行包含三个整数 $S,T$ 和 $K$ ，分别表示起点 $S$ ，终点 $T$ 和第 $K$ 短路。

输出格式

输出占一行，包含一个整数，表示第 $K$ 短路的长度，如果第 $K$ 短路不存在，则输出 $−1$ 。

数据范围

$1≤S,T≤N≤1000,$
$0≤M≤10^4,$
$1≤K≤1000,$
$1≤L≤100$

输入样例：

输出样例：

注意

本题估价函数使用 $dijkstra$ 反向建边求终点到各点的距离作为估计值 $f[u]$ .

代码：

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#define PII pair<int, int>
#define PIII pair<int, PII>
#define x first
#define y second
using namespace std;
const int N = 1010, M = 2e5 + 10;

int n, m, S, T, K;
int h[N], rh[N], e[M], w[M], ne[M], idx;
int dist[N], cnt[N];
bool st[N];

void add(int h[], int a, int b, int c)
{
    e[idx] = b;
    w[idx] = c;
    ne[idx] = h[a];
    h[a] = idx++;
}

void dijkstra()
{
    // 存储距离和起点
    // 反向搜索，从终点开始，小根堆
    priority_queue<PII, vector<PII>, greater<PII>> heap;
    heap.push({0, T});
    memset(dist, 0x3f, sizeof dist);
    dist[T] = 0;
    
    while (heap.size())
    {
        auto t = heap.top();
        heap.pop();
        
        int ver = t.y;
        if (st[ver]) continue;
        st[ver] = true;
        
        for (int i = rh[ver]; ~i; i = ne[i])
        {
            int j = e[i];
            if (dist[j] > dist[ver] + w[i])
            {
                dist[j] = dist[ver] + w[i];
                heap.push({dist[j], j});
            }
        }
    }
}

int astar()
{
    // {当前距离+估计到终点的距离, {当前距离, 当前节点}}
    priority_queue<PIII, vector<PIII>, greater<PIII>> heap;
    heap.push({dist[S], {0, S}});
    
    while (heap.size())
    {
        auto t = heap.top();
        heap.pop();
        
        int ver = t.y.y, distance = t.y.x;
        cnt[ver]++;
        
        //如果终点已经被访问过k次了, 则此时的ver就是终点T, 返回答案
        if (cnt[T] == K) return distance;
        
        for (int i = h[ver]; ~i; i = ne[i])
        {
            int j = e[i];
            /* 
            如果走到一个中间点都cnt[j]>=K, 则说明j已经出队k次了, 且astar()并没有return distance,
            说明从j出发找不到第k短路(让终点出队k次)，
            即继续让j入队的话依然无解，
            那么就没必要让j继续入队了
            */
            
            if (cnt[j] < K)
            {
                // 按 真实值+估计值 = d[j]+f[j] = dist[S->t] + w[t->j] + dist[j->T] 堆排
                // 真实值 dist[S->t] = distance+w[i]
                heap.push({distance + w[i] + dist[j], {distance + w[i], j}});
            }
        }
    }
    
    return -1;
}

int main()
{
    cin >> m >> n;
    
    memset(h, -1, sizeof h);
    memset(rh, -1, sizeof rh);
    
    for (int i = 0; i < n; i++){
        int a, b, c;
        cin >> a >> b >> c;
        add(h, a, b, c);
        add(rh, b, a, c);
    }
    
    cin >> S >> T >> K;
    
    // 起点==终点时 则d[S→S] = 0这种情况就要舍去, 总共第K大变为总共第K+1大 
    if (S == T) K++;
    
    // 从各点到终点的最短路距离 作为估计函数f[u]
    dijkstra();
    
    cout << astar() << endl;
    
    return 0;
}

7.2 八数码

在一个 $3×3$ 的网格中， $1∼8$ 这 $8$ 个数字和一个 X 恰好不重不漏地分布在这 $3×3$ 的网格中。

例如：

1 2 3
X 4 6
7 5 8

在游戏过程中，可以把 X 与其上、下、左、右四个方向之一的数字交换（如果存在）。

我们的目的是通过交换，使得网格变为如下排列（称为正确排列）：

1 2 3
4 5 6
7 8 X

例如，示例中图形就可以通过让 X 先后与右、下、右三个方向的数字交换成功得到正确排列。

交换过程如下：

1 2 3   1 2 3   1 2 3   1 2 3
X 4 6   4 X 6   4 5 6   4 5 6
7 5 8   7 5 8   7 X 8   7 8 X

把 X 与上下左右方向数字交换的行动记录为 u、d、l、r。

现在，给你一个初始网格，请你通过最少的移动次数，得到正确排列。

输入格式

输入占一行，将 $3×3$ 的初始网格描绘出来。
例如，如果初始网格如下所示：

1 2 3 
x 4 6 
7 5 8

则输入为：1 2 3 x 4 6 7 5 8