基础算法
基础算法
1. 快速排序
快排属于分治算法,分治算法都有三步:
- 分成子问题
- 递归处理子问题
- 子问题合并
主要步骤:
- 确定分界点,可以任选 a[l],a[r],a[(l + r) / 2] 其中一个作为分界点。
- 设置两个头尾指针 i, j,初始化 i = l - 1, j = r + 1 (避免发生边界问题导致死循环) ,向中间移动。每次循环都先将 i 右移和 j 左移,然后判断,如果 a[i] > a[j] 且 i < j,就交换 a[i] 和 a[j].
- 最后根据分界点分别递归左右两部分。
快排的一般写法如下:
void quick_sort(int q[], int l, int r)
{
//递归的终止情况
if(l >= r) return;
//第一步:分成子问题
int i = l - 1, j = r + 1, x = q[(l + r) / 2];
while(i < j)
{
do i++; while(q[i] < x);
do j--; while(q[j] > x);
if(i < j) swap(q[i], q[j]);
}
//第二步:递归处理子问题
quick_sort(q, l, j);
quick_sort(q, j + 1, r);
//第三步:子问题合并.快排这一步不需要操作,但归并排序的核心在这一步骤
}2. 归并排序
运用双指针的思想,先递归再合并。
主要步骤:
- 确定分界点。与快排不同,归并每次都将中点作为分界点,将整个序列均分为两部分。mid = (l + r) / 2
- 递归排序。对两个子序列分别设置个指针 i, j,从头开始遍历,每次比较 a[i] 和 a[j],将小的放入一个临时序列 temp[] 中。如果有一部分遍历完了,而另一部分还有剩余,则将剩余那一部分直接接在临时序列的后面,因为剩下的这部分一定是大于前面的。
- 归并,合二为一。将临时序列放入原序列中。
归并的一般写法如下:
void merge_sort(int a[], int l, int r)
{
if (l >= r) return;
//确定中间分界点
int mid = (l + r) >> 1;
//两边递归
merge_sort(a, l, mid);
merge_sort(a, mid + 1, r);
int k = 0;
int i = l, j = mid + 1;
//比较左右两半边
while (i <= mid && j <= r)
if (a[i] < a[j]) temp[k++] = a[i++];
else temp[k++] = a[j++];
while (i <= mid)//左半边剩下的
temp[k++] = a[i++];
while (j <= r)//右半边剩下的
temp[k++] = a[j++];
//合并区间
for (i = l, j = 0; i <= r; i++, j++)
a[i] = temp[j];
}3. 二分算法
3.1 二分查找算法模板
二分模板一共有两个,分别适用于不同情况。
算法思路:假设目标值在闭区间 [l, r]中, 每次将区间长度缩小一半,当 l = r时,我们就找到了目标值。
版本1
当我们将区间 [l, r]划分成 [l, mid] 和 [mid + 1, r] 时,其更新操作是 r = mid 或者 l = mid + 1; ,计算 mid 时不需要加 1。
C++代码模板:
int bsearch_1(int l, int r)
{
while (l < r)
{
int mid = l + r >> 1;
if (a[mid] >= x) r = mid; //答案在左边界,要向下取整
else l = mid + 1; //找左端点
}
return l;
}版本2
当我们将区间 [l, r] 划分成 [l, mid - 1] 和 [mid, r] 时,其更新操作是 r = mid - 1 或者 l = mid; ,此时为了防止死循环,计算 mid 时需要加 1。
C++代码模板:
int bsearch_2(int l, int r)
{
while (l < r)
{
int mid = l + r + 1 >> 1;
if (a[mid] <= k) l = mid; //答案在右边界,要上取整
else r = mid - 1; //找右端点
}
return l;
}简单来说就是:
可以将模板 1 中的 check[mid] 换成a[mid] >= x ,用来查找大于等于 x 的第一个元素;
将模板 2 中的 check[mid] 换成 a[mid] <= x ,用来查找小于等于 x 的最后一个元素。
3.2 二分答案模板
一般来说,二分答案可以用来处理 “最大的最小” 或 “最小的最大” 的问题。
定义区间为闭区间 [l, r] ,每次只需判断答案是否需要更新(是否记下ans)和(可能的)答案在哪一侧(改 L 还是 R )即可。
int ans;
int find(int l, int r)
{
while (l <= r)
{
int mid = l + r >> 1;
if (check(mid)){
ans = mid; //如果条件成立则记下答案
r = mid - 1; //判断可能的答案更新区间
}
else l = mid + 1;
}
return ans;
}3.3 整数二分
【例二】A-B 数对
题目描述:给出一串数以及一个数字 C ,要求计算出所有 A - B = C 的数对的个数(不同位置的数字一样的数对算不同的数对)。
这里使用库函数二分的写法:
依次枚举 A ,将问题转变成统计数列中 B + C 出现了多少次。先对数列排序,那么 B + C 会对应这个数列的连续一段,只要找到这个连续段的左端点和右端点即可。(需使用头文件 algorithm )
① lower_bound(begin, end, val) 可以在区间 [begin, end) 中找到 val 第一次出现的位置;
② upper_bound(begin, end, val) 可以在区间 [begin, end) 中找到 val 最后一次出现的位置的__后面一位__ 。
则这个数出现的次数就可以表示为 upper_bound() - lower_bound() ,时间复杂度为 O(nlogn).
#include <iostream>
#include <algorithm>
#define ll long long
using namespace std;
const int N = 2e5 + 10;
int n, c;
ll a[N];
int main()
{
cin >> n >> c;
for (int i = 0; i < n; i++) cin >> a[i];
sort(a, a + n);
ll tot = 0;
for (int i = 0; i < n; i++)
tot += upper_bound(a, a + n, a[i] + c) - lower_bound(a, a + n, a[i] + c);
cout << tot << endl;
return 0;
}3.4 浮点数二分
bool check(double x) {/* ... */} // 检查x是否满足某种性质
double bsearch_3(double l, double r)
{
const double eps = 1e-6; // eps 表示精度,取决于题目对精度的要求
while (r - l > eps)
{
double mid = (l + r) / 2;
if (check(mid)) r = mid;
else l = mid;
}
return l;
}4. 高精度算法
4.1 高精度加法
给定两个正整数(不含前导0),计算它们的和。
(C = A + B,A >= 0, B >= 0)
代码如下:
#include <iostream>
#include <vector>
using namespace std;
const int N = 1e6 + 10;
// C = A + B
vector<int> add(vector<int> &A, vector<int> &B) //加上&直接搜索数组A和B,不用全部遍历,节省时间
{
vector<int> C;
int t = 0; //进位,低位满10向高位进位,低位变为0
for (int i = 0; i < A.size() || i < B.size(); i++){
//两个if把两个数组相同位上的数相加
if (i < A.size())
t += A[i];
if (i < B.size())
t += B[i];
//把相加后的结果除以10求余,压入C数组中
C.push_back(t % 10);
//t再除以10,放入高位
t /= 10;
}
//如果最高位有数,则压入C数组中
if (t)
C.push_back(t);
//最后返回C数组
return C;
}
int main(){
string a, b;
vector<int> A, B;
cin >> a >> b; //例如 a = "123456"
for (int i = a.size() - 1; i >= 0; i--)
A.push_back(a[i] - '0'); //倒序存放, 数组A = [6, 5, 4, 3, 2, 1]
for (int i = b.size() - 1; i >= 0; i--)
B.push_back(b[i] - '0'); //同理, 数组B也是从低位(个位)存储, 从小到大
//使用auto编译器会自动判断数据是什么类型
auto C = add(A, B);
for (int i = C.size() - 1; i >= 0; i--)
printf("%d", C[i]);
return 0;
}4.2 高精度减法
给定两个正整数(不含前导0),计算它们的差,计算结果可能为负数。
1、前提:
C = A - B,满足 A >= B,A >= 0,B >= 0 (如果 B >= A,则将其转化为 -(B - A) )
2、代码段:(只考虑正数的情况)
#include <iostream>
#include <vector>
using namespace std;
//判断是否有 A >= B
bool cmp(vector<int> &A, vector<int> &B)
{
//A长度不等于B,若A大于B,返回true,否则返回false
if (A.size() != B.size())
return A.size() > B.size();
//因为是倒序数组,高位在后面,所以从后遍历
//如果A > B, 返回true,否则返回flase
for (int i = A.size() - 1; i >= 0; i--){
if (A[i] != B[i])
return A[i] > B[i];
}
return true;
}
// C = A - B
vector<int> sub(vector<int> &A, vector<int> &B) //加上&直接搜索数组A和B,不用全部遍历,节省时间
{
vector<int> C;
//定义一个借位的情况
int t = 0;
for (int i = 0; i < A.size(); i++){
//t = A的这一位数
t = A[i] - t;
//判断B在这一位上有没有数,如果有,则减去B[i]
if (i < B.size())
t -= B[i];
//这种写法包含了两种情况:如果t >= 0, 则直接减;若t < 0, 则向高位借位(即t + 10)后再减
//将这一位相减后的结果压入C中
C.push_back((t + 10) % 10);
if (t < 0) //t < 0,需要借位,标记为1
t = 1;
else //t >= 0,不需要借位,标记为0
t = 0;
}
//删除前导0
while (C.size() > 1 && C.back() == 0)
C.pop_back();
//最后返回C数组
return C;
}
int main(){
string a, b;
vector<int> A, B;
cin >> a >> b; //例如 a = "123456"
for (int i = a.size() - 1; i >= 0; i--)
A.push_back(a[i] - '0'); //倒序存放, 数组A = [6, 5, 4, 3, 2, 1]
for (int i = b.size() - 1; i >= 0; i--)
B.push_back(b[i] - '0'); //同理, 数组B也是从低位(个位)存储, 从小到大
//如果A > B,返回A - B
if (cmp(A, B)){
auto C = sub(A, B);
for (int i = C.size(); i >= 0; i--)
printf("%d", C[i]);
}
//否则返回 -(B - A)
else {
auto C = sub(B, A);
printf("-");
for (int i = C.size(); i >= 0; i--)
printf("%d", c[i]);
}
return 0;
}4.3 高精度整数乘法
给定两个非负整数(不含前导0)A 和 B,要求计算 A × B 的值
一般是 高精 × 低精,用 A × b 表示
(C = A * b,A >= 0,b >= 0)
代码如下:
#include <iostream>
#include <vector>
using namespace std;
//C = A * b
vector<int> mul(vector<int> &A, int b)
{
vector<int> C;
int t = 0;
for (int i = 0; i < A.size() || t; i++)
{
if (i < A.size())
t += A[i] * b;
//同加法一样处理进位,逐位压入数组中
C.push_back(t % 10);
t /= 10;
}
//删除前导0
while (C.size() > 1 && C.back() == 0)
C.pop_back();
return C;
}
int main()
{
string a;
int b;
cin >> a >> b;
vector<int> A;
for (int i = a.size() - 1; i >= 0; i--) //倒序插入
A.push_back(a[i] - '0');
auto C = mul(A, b);
for (int i = C.size() - 1; i >= 0; i--) //倒序输出
printf("%d", C[i]);
return 0;
}4.4 高精度整数除法
给定两个非负整数(不含前导0)A 和 B,要求计算 A / B 的商和余数 (第一行输出所求的商,第二行输出所求余数)
一般是 高精 ÷ 低精,用 A ÷ b 表示
(A / b = C ··· r,A >= 0,b > 0)
代码如下:
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
vector<int> div(vector<int> &A, int b, int &t) //传入t的地址,便于直接对余数进行处理
{
vector<int> C;
t = 0;
for (int i = A.size() - 1; i >= 0; i--)
{
//将上次的余数×10再加上当前位的数字,得到该位的被除数
t = t * 10 + A[i];
//所得即为商在这一位的数字
C.push_back(t / b);
t %= b;
}
//由于在除法运算中,从高位到低位运算,因此前导0在数组前面,所以需要将其翻转,将前导0置于尾部,从而便于删除前导0
reverse(C.begin(), C.end());
//删除前导0
while (C.size() > 1 && C.back() == 0)
C.pop_back();
return C;
}
int main()
{
string a;
int B;
cin >> a >> B;
vector<int> A;
for (int i = a.size() - 1; i >= 0; i--)
A.push_back(a[i] - '0');
int t; //t为余数
auto C = div(A, B, t);
for (int i = C.size() - 1; i >= 0; i--)
cout << C[i];
cout << endl << t << endl;
return 0;
}5. 前缀和与差分
5.1 一维前缀和
S[i] = a[1] + a[2] + ... a[i]
a[l] + ... + a[r] = S[r] - S[l - 1]5.2 二维前缀和
S[i, j] = 第i行j列格子左上部分所有元素的和
以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵的和为:
S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]5.3 一维差分
给区间[l, r]中的每个数加上c:B[l] += c, B[r + 1] -= c5.4 二维差分
给以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵中的所有元素加上c:
S[x1, y1] += c, S[x2 + 1, y1] -= c, S[x1, y2 + 1] -= c, S[x2 + 1, y2 + 1] += c6. 位运算
6.1 位运算符
位运算符作用于位,并逐位执行操作。
| 符号 | 描述 | 运算规则 |
|---|---|---|
| & | 与 | 两个位都为1时,结果才为1 |
| | | 或 | 两个位都为0时,结果才为0 |
| ^ | 异或 | 两个位相同为0,不同为1 |
| ~ | 取反 | 0变1,1变0 |
| << | 左移 | 各二进位全部左移若干位,高位丢弃,低位补0 |
| >> | 右移 | 各二进位全部右移若干位,对无符号数,高位补0,有符号数,各编译器处理方法不一样,有的补符号位(算术右移),有的补0(逻辑右移) |
6.2 用途
1、按位与 (&)
运算规则(全为 1,才为1)
| 0 & 0 = 0 | 0 & 1 = 0 | 1 & 0 = 0 | 1 & 1 = 1 |
|---|
注意:负数按补码形式参加按位与运算。
(1)清零
如果想将一个单元清零,使其全部二进制位为 0,只要__与一个各位都为零的数值相与__,结果为零。
(2)取一个数的指定位
比如取数 X = 1010 1110 的低 4 位,只需要另找一个数 Y,令 Y 的低 4 位为 1,其余位为 0,即 Y = 0000 1111,然后将 X 与 Y 进行按位与运算(X & Y = 0000 1110)即可得到 X 的指定位。
(3)判断奇偶
只要根据最未位是 0 还是 1 来决定,为 0 就是偶数,为 1 就是奇数。因此可以用 if ((a & 1) == 0) 代替 if (a % 2 == 0) 来判断 a 是不是偶数。
2、按位或 (|)
运算规则(全为 0,才为 0)
| 0 | 0 = 0 | 0 | 1 = 1 | 1 | 0 = 1 | 1 | 1 = 1 |
|---|
(1)常用来对一个数据的某些位设置为1
比如将数 X = 1010 1110 的低 4 位设置为 1,只需要另找一个数 Y,令 Y 的低 4 位为 1,其余位为 0,即 Y = 0000 1111,然后将 X 与 Y 进行按位或运算(X | Y = 1010 1111)即可得到。
3、按位异或 (^)
运算规则(相同为 0,不同为 1)
| 0 ^ 0 = 0 | 0 ^ 1 = 1 | 1 ^ 0 = 1 | 1 ^ 1 = 0 |
|---|
(1)翻转指定位
比如将数 X = 1010 1110 的低 4 位进行翻转,只需要另找一个数 Y,令 Y 的低 4 位为 1,其余位为 0,即 Y = 0000 1111,然后将 X 与 Y 进行异或运算(X ^ Y = 1010 0001)即可得到。
(2)与 0 相异或值不变
例如:1010 1110 ^ 0000 0000 = 1010 1110
(3)交换两个数
当 x == y 时,直接异或运算进行整数交换后,会导致 x = 0, y = x.
为避免这种情况,必须首先判断两个数是否相等。
void swap(int &a, int &b){
if (a != b){
a ^= b;
b ^= a;
a ^= b;
}
}4、按位取反 (~)
运算规则(0 变 1,1 变 0)
| ~1 = 0 | ~0 = 1 |
|---|
(1)使一个数的最低位为 0
使 x 的最低位为 0,可以表示为:a & ~1 。~1 的值为 1111 1111 1111 1110 ,再按 与 运算,最低位一定为 0。因为 ~ 运算符的优先级比算术运算符、关系运算符、逻辑运算符和其他运算符都高。
5、左移 (<<)
定义:将一个运算对象的各二进制位全部左移若干位(左边的二进制位丢弃,右边补0)。
设 a = 1010 1110,a = a << 2 将 a 的二进制位 左移2位、右补0,即得 a = 1011 1000。
若左移时舍弃的高位不包含 1,则每左移一位,相当于该数乘以 2 。比如 左移 k 位,即乘上 2k .
6、右移 (>>)
定义:将一个数的各二进制位全部右移若干位,正数左补 0 ,负数左补 1 ,右边丢弃。
例如:a = a >> 2 将 a 的二进制位右移 2 位,左补 0 或者 左补 1 得看被移数是正还是负。
操作数每右移一位,相当于该数除以 2。比如 右移 k 位,即除以 2k .
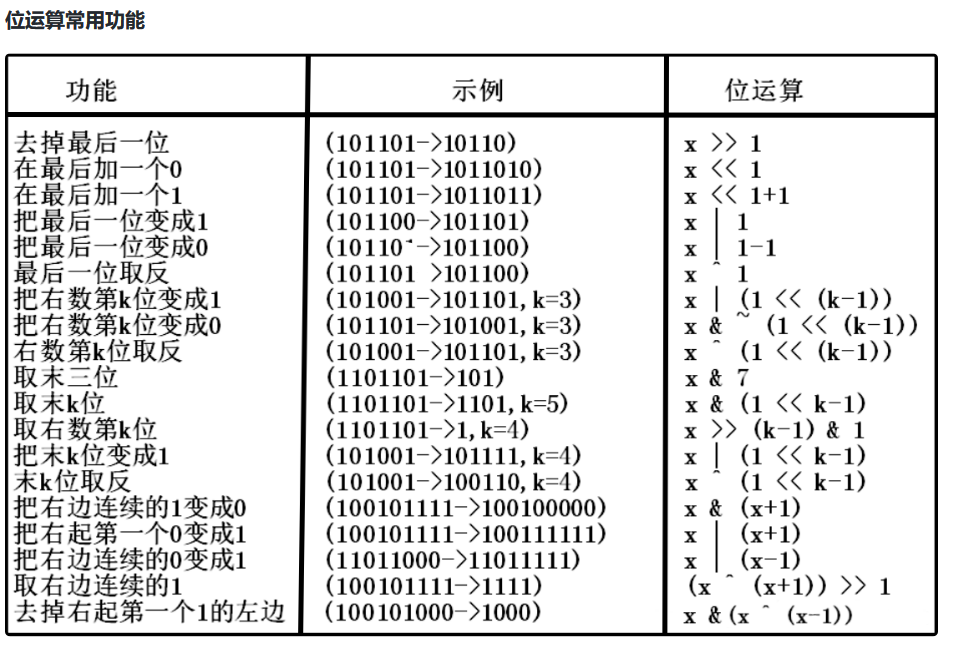
6.3 例题
【例题一】n 的二进制表示中第 k 位数
思路:先把第 k 位数字移动到最后一位,n 右移 k 位,即 n >> k ,再看个位是几,用 n & 1 ,合并两步后,即 n >> k & 1 .
例如求 10 的二进制表示,代码如下:
#include <iostream>
using namespace std;
int main()
{
int n = 10; //10的二进制表示为4位数
for (int k = 3; k >= 0; k--)
cout << (n >> k & 1);
return 0;
}输出如下:
1010【例题二】二进制中1的个数
给定一个长度为 1 的数列,请你求出数列中每个数的二进制表示中 1 的个数。
输入格式
第一行包含整数 n .
第二行包含 n 个整数,表示整个数列
输出格式
共一行,包含 n 个整数,其中的第 i 个数表示数列中的第 i 个数的二进制表示中 1 的个数。
思路:使用 lowbit(x) 来解决,其表达式为 x & -x ,其中 -x 表示补码,即源码取反加 1 ,-x = (~x + 1)。
作用:返回 x 的最后一位 1,比如 x = 1010, 则 lowbit(x) = 10 ,x = 101000, 则 lowbit(x) = 1000 .
代码如下:
#include <iostream>
using namespace std;
const int N = 100010;
int lowbit(int x)
{
return x & -x;
}
int main()
{
int n;
cin >> n;
while (n--){
int x;
cin >> x;
int res = 0;
while (x){
x -= lowbit(x);
res++;
}
cout << res << " ";
}
return 0;
}7. 双指针算法
for (int i = 0, j = 0; i < n; i++)
{
while (j < i && check(i, j)) j++;
// 具体问题的逻辑
// 例如求长度
res = max(res, i - j + 1);
}
常见问题分类:
(1) 对于一个序列,用两个指针维护一段区间
(2) 对于两个序列,维护某种次序,比如归并排序中合并两个有序序列的操作8. 离散化
vector<int> alls; // 存储所有待离散化的值
sort(alls.begin(), alls.end()); // 将所有值排序
alls.erase(unique(alls.begin(), alls.end()), alls.end()); // 去掉重复元素
// 二分求出x对应的离散化的值
int find(int x) // 找到第一个大于等于x的位置
{
int l = 0, r = alls.size() - 1;
while (l < r)
{
int mid = l + r >> 1;
if (alls[mid] >= x) r = mid;
else l = mid + 1;
}
return r + 1; // 映射到1, 2, ...n
}9. 区间合并
// 将所有存在交集的区间合并
void merge(vector<PII> &segs)
{
vector<PII> res;
sort(segs.begin(), segs.end());
int L = -2e9, R = -2e9;
for (auto seg : segs)
if (R < seg.first)
{
if (st != -2e9) res.push_back({L, R});
L = seg.first, R = seg.second;
}
else R = max(R, seg.second);
if (L != -2e9) res.push_back({L, R});
segs = res;
}