二叉搜索树中第K小的元素

230.二叉搜索树中第K小的元素

题意

给定一个二叉搜索树的根节点 root，和一个整数 k，请你设计一个算法查找其中第 k 小的元素（从 $1$ 开始计数）。

思路

利用二叉搜索树的重要性质：二叉搜索树的中序遍历为递增序列。

也就是说，本题可被转化为求中序遍历的第 k 个节点。

转化为求中序遍历的第k个节点

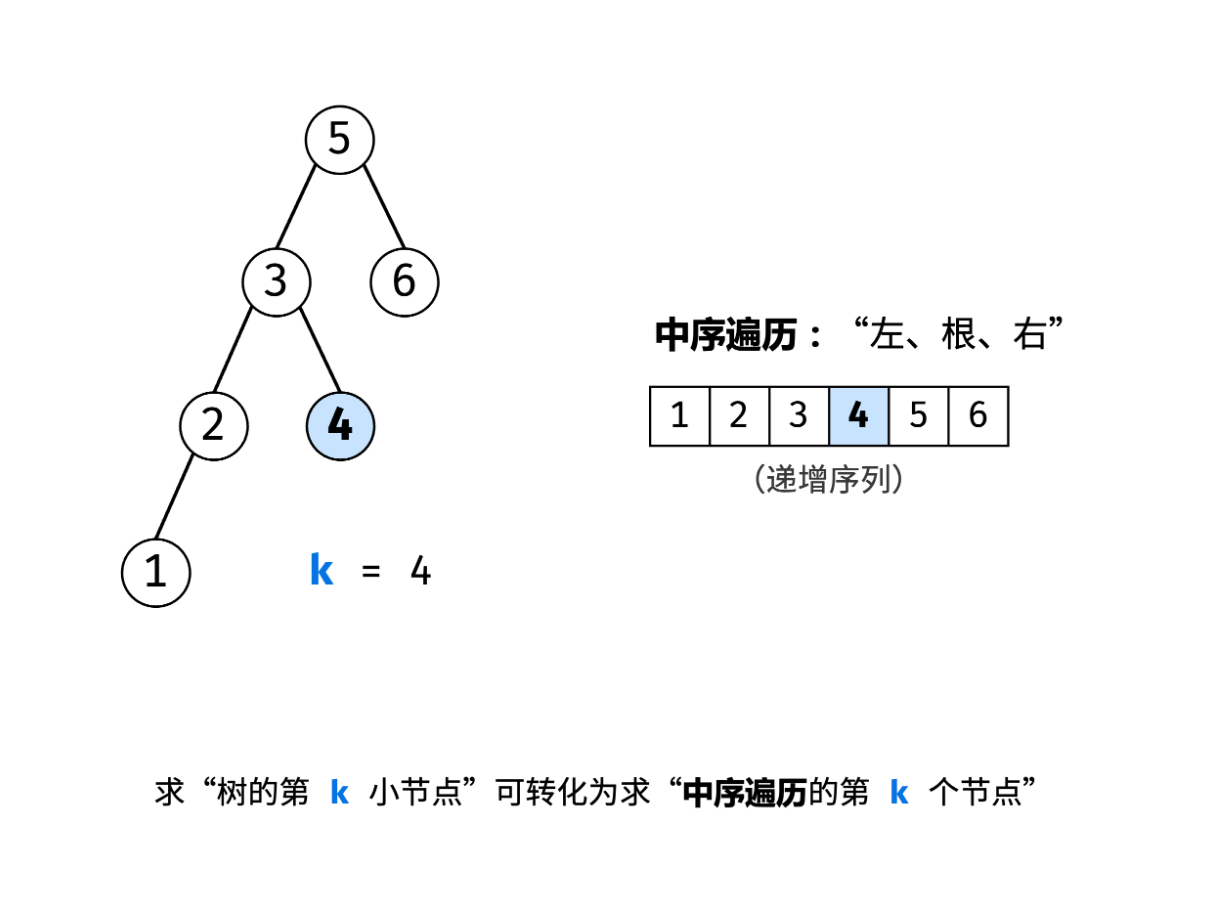
使用 ans 记录并更新遍历到的节点，当 k = 0 时，返回即可。

代码：

class Solution {
    int k;
    int ans;

    void dfs(TreeNode root) {
        if (root == null) return;

        dfs(root.left);
        if (k == 0) return;
        if (--k == 0) ans = root.val;
        dfs(root.right);
    }

    public int kthSmallest(TreeNode root, int k) {
        this.k = k;
        dfs(root);
        return ans;
    }
}

进阶

如果二叉搜索树经常被修改（插入/删除操作）并且你需要频繁地查找第 k 小的值，你将如何优化算法？

思路

在前面的方法中，我们之所以需要中序遍历前 k 个元素，是因为我们不知道子树的结点数量，不得不通过遍历子树的方式来获知。为了优化算法，我们可以记录每个子树的结点数。对于每个结点，先记录左子树中的结点数 leftNodes，然后缩小查找第 k 小的元素的范围。

判断：

• 如果 leftNodes = k − 1，则当前结点值即为第 k 小的元素，返回当前结点值。
• 如果 leftNodes > k − 1，则第 k 小的元素一定在左子树中，因此在左子树中寻找第 k 小的元素。
• 如果 leftNodes < k − 1，则第 k 小的元素一定在右子树中，由于以当前结点为根结点的子树中的大于右子结点值的结点数等于 leftNodes + 1，因此在右子树中寻找第 k − leftNodes − 1 小的元素。

代码

class Solution {
    // 左右子树返回信息只需要节点数，无需额外定义数据结构
    public int countNodes(TreeNode root) {
        if(root == null) return 0;

       // 递归处理左右子树并接收返回值
        int leftNodes = countNodes(root.left);
        int rightNodes = countNodes(root.right);
       // 判断分析本层递归返回值的具体值
        return leftNodes + rightNodes + 1;
    }

    public int kthSmallest(TreeNode root, int k) {
        int leftNodes = countNodes(root.left);
        if (leftNodes < k - 1) {  // 答案存在右子树中
            return kthSmallest(root.right,k - leftNodes - 1);
        } else if (leftNodes == k - 1) {
            return root.val;
        } else {
            return kthSmallest(root.left,k);
        }
    }
}